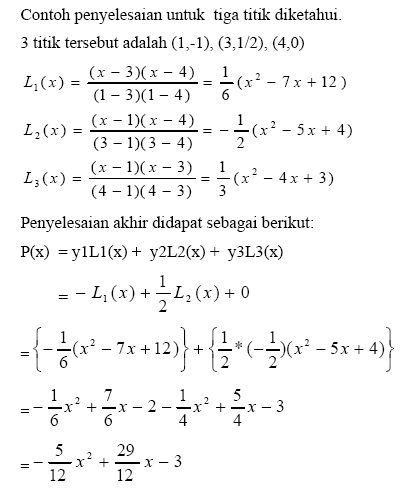Metode Newton Raphson merupakan salah satu metode yang tangguh dalam mencari nilai hampiran akar untuk persamaan non linier. Tetapi, tidaksemua fungsi dapat mudah diturunkan. Oleh karena itu, maka metode Newton Raphson ini dimodifikasi, dan diberi nama metode Secant. Berbeda dengan metode Newton Raphson, pada metode secant tidak diperlukan turunan pertama dari
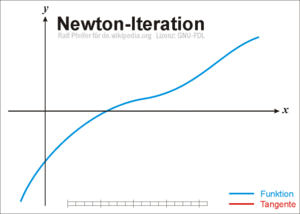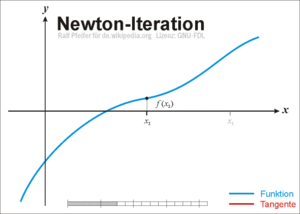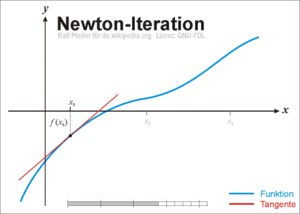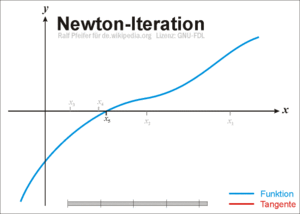
fungsi non liniernya, tetapi diperlukan dua buah nilai awal. Berikut ilustrasi grafiknya.

Metode Numerik - Ilustrasi Metode Secant
Sehingga diperoleh prosedur iterasinya adalah sebagai berikut:

Proses Iterasi akan berhenti apabila memenuhi kondisi dibawah ini.
 Contoh:
Contoh:
Hitung Akar persamaan non linier berikut ini :

dengan ε =n 0.00001. Tebakan nilai awal akar x0=0.5 dan x1=1.
Penyelesaian

Implementasi Metode Secant dalam bahasa C
#include
#include
double f(double x)
{
return cos(x) - x*x*x;
}
double SecantMethod(double xn_1, double xn, double e, int m)
{
int n;
double d;
for (n = 1; n <= m; n++)
{
d = (xn - xn_1) / (f(xn) - f(xn_1)) * f(xn);
if (fabs(d) < e)
return xn;
xn_1 = xn;
xn = xn - d;
}
return xn;
}
int main(void)
{
printf("%0.15f\n", SecantMethod(0, 1, 5E-11, 100));
return 0;
}
Implementasi Metode Secant Menggunakan Matlab
function metodesecant;
clc;
clear;
disp('Program Metode Secant');
disp('=============================');
E=0.0001;
x0=input('Masukkan X0 :');
xb=input('Masukkan X1 :');
i=0;
M=9;
disp('_______________________________________________');
disp(' i xi f(xi) epsilon');
disp('_______________________________________________');
while (E
fx=exp(x0)-5*x0^2;
fxb=exp(xb)-5*xb^2;
d = xb - (fxb*(xb-x0)/(fxb-fx));
M=abs(x0-xb);
x0 = xb;
xb = d;
i=i+1;
fprintf('%3.0f %12.6f %12.6f %12.6f\n',i,xb,fx,M);
end;
disp('_______________________________________________');
fprintf('Akarnya Adalah = %10.8f\n',xb);
end
Hasilnya
Program Metode Secant
=============================
Masukkan X0 :0.5
Masukkan X1 :1
_______________________________________________
i xi f(xi) epsilon
_______________________________________________
1 0.574376 0.398721 0.500000
2 0.596731 -2.281718 0.425624
3 0.605533 0.126483 0.022354
4 0.605265 0.035734 0.008803
5 0.605267 -0.001123 0.000268
6 0.605267 0.000009 0.000002
_______________________________________________
Akarnya Adalah = 0.60526712